If ![]() is a given partial order on I, then the set
of all
is a given partial order on I, then the set
of all ![]() -hereditary properties will be denoted by
-hereditary properties will be denoted by
![]()
![]() .
As special cases the set
.
As special cases the set ![]()
![]() of all
hereditary properties will be denoted by
of all
hereditary properties will be denoted by ![]() and
the set of all additive hereditary properties will be denoted
by
and
the set of all additive hereditary properties will be denoted
by ![]() a. The first results in this section describe the
structure of these sets, ordered by inclusion.
a. The first results in this section describe the
structure of these sets, ordered by inclusion.
Theorem 1 ([17])
The partially ordered sets (![]() ,
, ![]() )
and (
)
and (![]() a,
a,
![]() ) are distributive lattices.
) are distributive lattices.
Note that ![]() is closed under (arbitrary) intersections and
unions
while
is closed under (arbitrary) intersections and
unions
while ![]() a is closed under (arbitrary) intersections. Hence
the properties in
a is closed under (arbitrary) intersections. Hence
the properties in ![]() and in
and in ![]() a form closure systems
(see [3]). From this it follows that the lattices in
Theorem 1 are complete. Hence we have
a form closure systems
(see [3]). From this it follows that the lattices in
Theorem 1 are complete. Hence we have
Theorem 2 [17]
The partially ordered sets (![]() ,
, ![]() )
and (
)
and (![]() a,
a, ![]() ) are complete distributive lattices
with least element
) are complete distributive lattices
with least element ![]() and greatest element I.
and greatest element I.
It should be noted that (![]() a ,
a , ![]() ) is not
a sublattice of (
) is not
a sublattice of (![]() ,
, ![]() ) since the join of
properties in the former is not the union of these properties.
Therefore the distributivity of (
) since the join of
properties in the former is not the union of these properties.
Therefore the distributivity of (![]() a,
a, ![]() )
is not completely trivial. In [17], [70] an isomorphism
between (
)
is not completely trivial. In [17], [70] an isomorphism
between (![]() a,
a, ![]() ) and a suitable lattice of sets of
connected graphs is used to prove it.
) and a suitable lattice of sets of
connected graphs is used to prove it.
For a graph H![]() I,
I,
![]() H denotes the class of all graphs that
admit homomorphisms to H. Such classes of graphs are called
hom-properties or colour classes and were investigated e.g.,
in [55], [61],
[62], [77] and [102].
It was pointed out that they play an
interesting role in the lattice (
H denotes the class of all graphs that
admit homomorphisms to H. Such classes of graphs are called
hom-properties or colour classes and were investigated e.g.,
in [55], [61],
[62], [77] and [102].
It was pointed out that they play an
interesting role in the lattice (![]() a,
a,![]() ).
).
Theorem 3 [60]
The hom-properties form a sublattice of ![]() a.
a.
We will present more information about the structure of the sublattice of hom-properties in Section 3.
For a given nonnegative integer k, let
Since ![]() ka is also a closure system we have
ka is also a closure system we have
Theorem 4[17]
The ordered set (![]() ka ,
ka , ![]() ) is a complete
distributive lattice and it is a sublattice of (
) is a complete
distributive lattice and it is a sublattice of (![]() a ,
a ,
![]() ). Ok is the least element and
Ik
is the greatest element of (
). Ok is the least element and
Ik
is the greatest element of (![]() ka ,
ka , ![]() ).
).
Since the set ![]() forms a lattice with a set union and
a set intersection as operations it is natural to ask,
for any two hereditary properties P1
and P2,
what the completeness of P1
forms a lattice with a set union and
a set intersection as operations it is natural to ask,
for any two hereditary properties P1
and P2,
what the completeness of P1
![]() P2 and
P1
P2 and
P1 ![]() P2 is in terms of the completenesses
of P1 and
P2. Our next result answers
this question.
P2 is in terms of the completenesses
of P1 and
P2. Our next result answers
this question.
Theorem 5[17]
Let P1
and P2 be any nontrivial
hereditary properties of graphs. Then
c(P1
![]() P2)
= max{c(P1),
c(P2)}
and c(P1
P2)
= max{c(P1),
c(P2)}
and c(P1
![]() P2)
= min{c(P1),
c(P2)}.
P2)
= min{c(P1),
c(P2)}.
The algebraicity of these lattices will be discussed in Section 4.
F(P)= {G
![]() I : G
I : G
![]() P
but each proper subgraph H of G belongs
to P}.
P
but each proper subgraph H of G belongs
to P}.
Note that F(P) may be finite or infinite.
Some direct consequences of this definition are contained in the next lemma. It shows amongst others how a hereditary property can uniquely be determined by its set of minimal forbidden subgraphs.
Lemma 6.
Let P be a hereditary property. Then
(a) G ![]() P if and only if
no subgraph of G is in F(P).
P if and only if
no subgraph of G is in F(P).
(b) If P is additive, then
F(P) contains only connected
graphs.
The set of minimal forbidden subgraphs of each of the properties in Example 1, except for Dk and hom-properties, is easy to describe. A list of them is given in the following example.
Example 2.
Let Sn and Pn
to denote the star and the path on n vertices, respectively. Then
| F(O) | = | { K2 }, |
| F(Ok) | = | {H |
| F(Sk) | = | {Sk+2}, |
| F(Wk) | = | {Pk+2}, |
| F(Tk) | = | {H |
| F(Ik) | = | {Kk+2}. |
To characterize the set F(Dk)
we need some more notation. For a nonnegative integer k and a graph G, we denote
the set of all vertices of G of degree k+1 by M(G).
If S![]() V(G) is a cutset of vertices of G
and G1, . . . ,Gs, s
V(G) is a cutset of vertices of G
and G1, . . . ,Gs, s![]() 2
are the components of G - S, then the graph G - V(Gi) is denoted by
Hi, i=1, . . . ,s.
2
are the components of G - S, then the graph G - V(Gi) is denoted by
Hi, i=1, . . . ,s.
Theorem 7[67]
A graph G belongs to F(Dk)
if and only if G is connected, ![]() (G)
(G)
![]() k+1, V(G) - M(G)
is an independent set of vertices of G and for
each cutset S
k+1, V(G) - M(G)
is an independent set of vertices of G and for
each cutset S![]() V(G) - M(G) we have that
V(G) - M(G) we have that
![]() (Hi)
(Hi)![]() k for each i=1, . . . ,s.
k for each i=1, . . . ,s.
The characterization of the the forbidden graphs for a hom-property
![]() H
seems to be very complicated and it is known just for very particular choices
of the graph H (see [62]). Such choices of the graph H yields
to the properties which were already discussed in Example 2.
H
seems to be very complicated and it is known just for very particular choices
of the graph H (see [62]). Such choices of the graph H yields
to the properties which were already discussed in Example 2.
In the next theorem the following notation is useful.
If S is a set of graphs we write
min![]() [S]
for the set of graphs in
S that are
minimal with respect to the partial order
[S]
for the set of graphs in
S that are
minimal with respect to the partial order ![]() on
I.
Note that, in this notation, F(P) =
min
on
I.
Note that, in this notation, F(P) =
min![]() [I -
P] for any nontrivial hereditary property
P.
[I -
P] for any nontrivial hereditary property
P.
Theorem 8[17]
Let P1 and
P2 be any
nontrivial hereditary properties of graphs. Then
min![]() P2) =
P2) =
![]() [F(P1)
[F(P1)
![]() F(P2)],
F(P2)],
The completeness of a property is now described in terms of its forbidden subgraphs.
Theorem 9[17]
Let P be any nontrivial hereditary
property of graphs. Then
c(P)= min{|V(H)|-2 : H
![]() F(P)}.
F(P)}.
Inclusion between properties, and hence equality between properties, can also be described in terms of forbidden subgraphs.
Theorem 10[17]
Let P1 and
P2 be any nontrivial hereditary
properties. Then P1
![]() P2
if and only if for every H
P2
if and only if for every H![]() F(P2) there exists
a graph H'
F(P2) there exists
a graph H' ![]() F(P1) such
that H'
F(P1) such
that H' ![]() H.
H.
and the set of P-maximal graphs of order n by
Our next result follows immediately from these definitions.
Lemma 11.
Let P
be a nontrivial hereditary property. Then
![]() M(P) such that
G
M(P) such that
G![]() H.
H.
![]() M(P)n such that
G
M(P)n such that
G![]() H.
H.
![]() n
M(n,P).
n
M(n,P).
From the definition of P-maximal graphs and the completeness of a property we immediately deduce the following result.
Lemma 12. [21]
Let P be a nontrivial hereditary property. Then
![]() n
n ![]() c(P) + 1.
c(P) + 1.
![]() M(P),
H
M(P),
H ![]() M(P)
and G is a subgraph of H or H is a subgraph of G, then G = H.
M(P)
and G is a subgraph of H or H is a subgraph of G, then G = H.
It is natural, that Statement 2 of the previous lemma inspire us to introduce a more general concept---the generator of a hereditary (an additive hereditary) property. To be more exact, consider an arbitrary set X, a subset of I. It is quite easy to see,that the property
is hereditary, the property
is in addition additive and both are generated by the set X, called generator.
The previous lemma yields, that the set M(P) generates the
(additive) hereditary property P. On the other hand, it is not difficult
to see, that the set M(P) is neither the unique nor the minimal (with
respect to the set inclusion) generator of P. In fact, for any positive
integer k the sets
Mk=![]() n
n![]() k
M(n,P) and
M*k=
k
M(n,P) and
M*k=![]() n
n![]() k,n
k,n![]() 0(mod2)
M(n,P)
are generators of P too.
The concept of generator will be discussed, in more details and in general, with respect
to a partial order, in Section 4.
0(mod2)
M(n,P)
are generators of P too.
The concept of generator will be discussed, in more details and in general, with respect
to a partial order, in Section 4.
From the definitions follows, that there is a very strong dependence between the structure of minimal graphs and the structure of P-maximal graphs for a given hereditary property P. One can expect, that it is quite easy to deduce the structure of forbidden graphs when all P-maximal graphs are known and vice versa. Unfortunately, this problem seems to be very difficult even for such familiar hereditary properties as O2 (to be a bipartite graph) and D1 (to be a forest). Indeed, although the structure of the sets F(O2), F(D1), M(O2) and M(D1) is well described, there are known no general rules, which can be used for a transformation between F(O2) and M(O2), and F(D1) and M(D1).
However, the dependence can be expressed by means of a graph
theoretical invariant. In order to present it, we need the following
notation. If ![]() is any graph theoretical invariant, then the symbol
is any graph theoretical invariant, then the symbol
![]() (P) stands for
(P) stands for
Theorem 13[72]
Let ![]() (G) be a graph theoretical invariant satisfying:
(G) be a graph theoretical invariant satisfying:
Then for any graph G![]() (H)
is at most
(H)
is at most ![]() (G),
(G),
![]() I and for an arbitrary edge e from
the complement of G holds
I and for an arbitrary edge e from
the complement of G holds ![]() (G+e)
(G+e)![]()
![]() (G)+1.
(G)+1.
![]() M(n,P) with n
M(n,P) with n
![]() c(P)+ 2
holds the following:
c(P)+ 2
holds the following:
![]() (G)
(G)![]()
![]() (P)-1.
(P)-1.
The next lemma shows that inclusion between properties can also be described in terms of the corresponding sets of maximal graphs.
Lemma 14[21]
Let P1 and
P2 be any nontrivial hereditary
properties. Then P1
![]() P2
if and only if for every G
P2
if and only if for every G![]() M(P1) there is
a graph H
M(P1) there is
a graph H ![]() M(P2) such that
G
M(P2) such that
G ![]() H.
H.
The next lemma provides a criterion for the verification of P-maximal graphs in terms of the features of comparable hereditary properties.
Lemma 15[84]
Let P1 and
P2 be any
hereditary properties of graphs.
If P1![]() P2, G
P2, G![]() M(n,P2) and
G
M(n,P2) and
G![]() P1,
then G belongs to M(n,P1).
P1,
then G belongs to M(n,P1).
We now discuss the maximal graphs of order n
for some of the properties listed in Example 1.
In view of Lemma 12 we can restrict our attention
to a property P and an integer n with
n![]() c(P) + 2.
This is then our choice in each case of the following example.
c(P) + 2.
This is then our choice in each case of the following example.
Example 3.
Let n be a positive integer, n![]() c(P) + 2.
Then
c(P) + 2.
Then
| M(n,O) | = | { |
| M(n,Ok) | = | {Kr1} |
| M(n,{S}k) | = | {G |
| M(n,D1) | = | {G |
| M(n,T2) | = | {G |
| M(n,T3) | = | {G |
| M(n,I1) | = | {G |
The structure of maximal k-degenerate graphs has been studied extensively in [37], [64] and [75] and one description is given in the following theorem.
Theorem 16[64]
Let G=(V,E) be a graph of order n, n ![]() k+1, and v
k+1, and v ![]() V
be a vertex of degree k. Then G
V
be a vertex of degree k. Then G![]() M(n,Dk)
if and only if G-v
M(n,Dk)
if and only if G-v![]() M(n-1,Dk).
M(n-1,Dk).
The degree sequences of maximal k-degenerate graphs can also be characterized (see [15]). The characterization of graphs maximal with respect to hom-properties was obtained in [62] and will be presented in the Section 3.
We now introduce the notation max![]() [
S],
for a set S of graphs, to denote the set of graphs
in S that are maximal with respect to
the partial order
[
S],
for a set S of graphs, to denote the set of graphs
in S that are maximal with respect to
the partial order ![]() on I.
This concept is useful to describe
M(n,P1
on I.
This concept is useful to describe
M(n,P1
![]() P2)
and M(n,P1
P2)
and M(n,P1
![]() P2) in terms
of M(n,P1) and
M(n,P2).
P2) in terms
of M(n,P1) and
M(n,P2).
Theorem 17[84]
Let n be a positive integer and let
P1 and
P2 be hereditary properties of graphs. Then
![]() P2) =
max
P2) =
max![]() [M(n,P1)
[M(n,P1)
![]() M(n,P2)],
M(n,P2)],
![]() P2) =
max
P2) =
max![]() [{G
[{G![]() I :
there exists a pair of graphs H1
I :
there exists a pair of graphs H1 ![]() M(n,P1) and H2
M(n,P1) and H2
![]() M(n,P2)
such that G
M(n,P2)
such that G![]() H1 and G
H1 and G![]() H2,}].
H2,}].
A general extremal problem, in our terminology, can be formulated as follows. Given a hereditary property P with a family F(P) of forbidden subgraphs, find the numbers
The set of all P-maximal graphs of order n with exactly ex(n,P) edges is denoted by Ex(n,P). The members of Ex(n,P) are called P-extremal graphs. By the symbol Sat(n,P) we shall denote the set of all P-maximal graphs on n vertices with sat(n,P) edges. These graphs are called P-saturated.
A problem of such type was first formulated by Turán (see [95],[96]) and his original problem asked for the maximum number of edges in any graph of order n which does not contain the complete graph Kp (i.e. he was interested in the number ex(n,Ip-2)).
The following two theorems belong to the fundamental results of extremal graph theory.
Theorem 18[88]
If P is a hereditary property
with chromatic number ![]() (P),
then
(P),
then
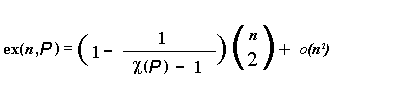
Theorem 19[58]
If P is a given hereditary property and
u = u(P) =
min{|V(F)|-
d = d(P) =
min{|E(F')|
then
![]() (F)-1 : F
(F)-1 : F![]() P}
P}
![]() F'
F'
![]() F
F![]() F(P)
is induced by a set S
F(P)
is induced by a set S![]() {x},
S
{x},
S![]() V(F)
is independent and |S|=|V(F)|-u-1,
x
V(F)
is independent and |S|=|V(F)|-u-1,
x![]() V(F)-S},
V(F)-S},
![]() un + (1/2)(d-1)(n-u)-
un + (1/2)(d-1)(n-u)-
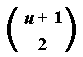 ,
if n is large enough.
,
if n is large enough.
As a consequence of the previous two theorems we immediately have
Corollary 20.
If P is a hereditary property of graphs and
sat(n,P)=ex(n,P) for every
positive n, then ![]() (P)=2.
(P)=2.
The hereditary properties with ![]() (P)=2
are called degenerate. It will turn out in the next sections that these properties play an
important role in the lattice
(P)=2
are called degenerate. It will turn out in the next sections that these properties play an
important role in the lattice ![]() a. We shall also deal with
degenerate hereditary properties, which have some tree among forbidden subgraphs.
As they position in the investigated lattice is also interesting, we shall
called them very degenerate - see [89].
a. We shall also deal with
degenerate hereditary properties, which have some tree among forbidden subgraphs.
As they position in the investigated lattice is also interesting, we shall
called them very degenerate - see [89].
The numbers ex(n,P) and sat(n,P) have been studied very extensively e.g., in [34], [35], [58], [80], [86], [87], [88], [97], and [84], but there are not many hereditary properties, for which the exact values of sat(n,P) and ex(n,P) are known. It seems that the determination of sat(n,P) is much more complicated than the estimation of the number ex(n,P). There are two important causes for this fact. Firstly, unlike the number ex(n,P), the behaviour of sat(n,P) is not monotone in general (see [58]). Secondly, the determination of ex(n,P) requires max-max optimization, while for the evaluation of sat(n,P) the min-max type of optimization is necessary.
It was pointed out that the language of the lattice of hereditary properties enables us to investigate the numbers ex(n,P) and sat(n,P) from another point of view and utilize the structure of the lattice instead of the concrete knowledge about P-maximal graphs (for more details see [84]).
The following assertions present some results of utilization of this method.
Theorem 21([84])
If P is a hereditary property, such that
Ok ![]() P
P ![]() Dk or
Dk
Dk or
Dk ![]() P
P ![]() Ik,
n
Ik,
n![]() k+1, then sat(n,P)
k+1, then sat(n,P)
![]() kn -
kn - 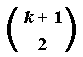 .
.
Theorem 22([84])
Let P be a hereditary property and let
D1
![]() P
P
![]() I1.
If the vertex-connectivity
I1.
If the vertex-connectivity ![]() (P)
(P)![]() 1, then
sat(n,P)=n-1.
1, then
sat(n,P)=n-1.