Contents
... Next ... ReferencesA Survey of Hereditary Properties of Graphs
All graphs considered are finite, simple, i.e., undirected, loopless and without multiple edges. For undefined concepts we refer the reader to [29], [8] and [17].
A graph property is a any isomorphism-closed subclass of graphs. Since we have in general no reason to distinguish between isomorphic copies of a graph, we use the notation I to denote the set of all unlabelled graphs. Therefore, by saying that H is a subgraph of G, we mean that H is isomorphic to a subgraph of G.
If P is a subset of I, then P will also
denote the property that a graph is a member of the set P.
We shall use the terms set of graphs and property of graphs
interchangeably. The symbol ![]() will
stand for the empty property, i.e. the subsets of I
containing no graphs. Properties I and
will
stand for the empty property, i.e. the subsets of I
containing no graphs. Properties I and ![]() are called trivial.
are called trivial.
By the join G1 + G2 + ... + Gn of n graphs G1,
G2, ... ,Gn we mean the graph consisting of disjoint copies of G1,
G2, ... ,Gn and all the edges between V(Gi) and V(Gj)
for all i![]() j. Every graph which is the
join of at least two graphs is called decomposable. A graph that is not
decomposable is called indecomposable. It is easy to see that a graph G is
decomposable if and only if its complement
j. Every graph which is the
join of at least two graphs is called decomposable. A graph that is not
decomposable is called indecomposable. It is easy to see that a graph G is
decomposable if and only if its complement ![]() is not connected. Then G is a join of the complements of
the components of
is not connected. Then G is a join of the complements of
the components of ![]() . Thus every
decomposable graph G can be expressed in a unique way as the join of indecomposable
graphs.
. Thus every
decomposable graph G can be expressed in a unique way as the join of indecomposable
graphs.
A homomorphism of a graph G to a graph H is a mapping f of the vertex set V(G)
into V(H) which preserves the edges, i.e., if e={u,v}![]() E(G) than f(e)={f(u),f(v)}
E(G) than f(e)={f(u),f(v)}![]() E(H).
E(H).
If a homomorphism of G to H exists, we say that G is homomorphic to H and
write G![]() H. It is easily seen that
in such case for the chromatic number the following inequality
H. It is easily seen that
in such case for the chromatic number the following inequality ![]() (G)<=
(G)<=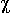 (H) holds.
(H) holds.
A property P is called additive if
for each graph G all of whose components have property P
it follows that G![]() P
too. Throughout the paper we let
P
too. Throughout the paper we let ![]() be a
partial order on the set I. A property P is said to be
be a
partial order on the set I. A property P is said to be ![]() -hereditary if, whenever G
-hereditary if, whenever G![]() P and H
P and H![]() G, then also H
G, then also H![]() P. A property P is induced hereditary if it is
P. A property P is induced hereditary if it is ![]() -hereditary with respect to the relation
-hereditary with respect to the relation
![]() to be an induced subgraph
and P is hereditary if it is
to be an induced subgraph
and P is hereditary if it is ![]() -hereditary with respect to the relation
-hereditary with respect to the relation ![]() to be a subgraph (some authors
prefer the term monotone instead of hereditary, see [26],
[82]). In the first three sections of this survey we shall
concentrate on additive hereditary properties; properties that are hereditary with respect
to other partial orderings are the subject of study in later sections.
to be a subgraph (some authors
prefer the term monotone instead of hereditary, see [26],
[82]). In the first three sections of this survey we shall
concentrate on additive hereditary properties; properties that are hereditary with respect
to other partial orderings are the subject of study in later sections.
Hereditary properties were studied extensively (see e.g. [7], [17], [23], [25], [26], [48], [64], [83] and [101]).
Example 1. We list some important hereditary properties, using partially the notation of [17].
| O | = | {G |
|
| Ok | = | {G |
|
| Sk | = | {G | |
| Wk | = | {G |
|
| Dk | = | {G G }, G }, |
|
| Tk | = | {G |
|
| Ik | = | {G |
|
| H | = | {G |
It is easy to see that for k=1 the properties O1, S1 and W1 are equal each other.
Let P be a nontrivial hereditary property.
Then there is a nonnegative integer c(P) such
that Kc(P)+1![]() P but Kc(P)+2
P but Kc(P)+2![]() P -- it is
called the completeness of P. Obviously
P -- it is
called the completeness of P. Obviously
c(Ok) = c(Sk) = c(Wk) = c(Dk) = c(Tk) = c(Ik) = k
and c(P) = 0 if and only if P=O.
By a partition of a set S into n parts we mean an unordered family { S1,
S2, ... , Sn } of pairwise disjoint subsets of S with ![]() Si = S. Note that
some of the Si's may be empty. In the case that an ordered partition is
required we shall denote the ordered partition by [S1, S2, ... , Sn].
Si = S. Note that
some of the Si's may be empty. In the case that an ordered partition is
required we shall denote the ordered partition by [S1, S2, ... , Sn].
In Section 2 we investigate the lattice of additive and hereditary properties of graphs. It is shown how minimal forbidden subgraphs and maximal graphs are used to characterize properties.
In Section 3 we discuss vertex partitions of graphs. Reducibility of properties plays a major role in this section and the relationship between this concept and the existence of uniquely partitionable graphs is explained. The concept of minimal reducible bounds are shown to provide a wealth of difficult problems.
In Section 4 lattices arising from other partial orderings on I are studied. These lattices can be used to explain many seemingly unrelated concepts and results from Graph Theory.
Section 5 is devoted to show how many known invariants of graphs can be related to chains of such properties of graphs.
In Section 6 we list some important results concerning the complexity of partition problems related to properties of graphs (see also [98]).
1997